Lecture 19: The Message Passing Interface

../_images/L19-sp22-title.png Lecture 19 slides Lecture 19 panopto Podcast

(Recorded on 2022-05-31)

We continue to develop the message passing paradigm for distributed memory parallel computing. Laplace’s equation is part of the HPC canon so we do a deep dive on approaches for solving Laplace’s equation (iteratively) with MPI – which leads to the the compute-communicate (aka BSP) pattern. We also provide other solutions for communication using non-blocking operations. We introduce more MPI collectives in this lecture.

Non-blocking operations

Other than using blocking operations (send and recv) of MPI, we can also send messages using non-blocking operations: MPI_Isend, MPI_Irecv, and MPI_Wait (or MPI_Waitall). The non-blocking operations (send and receive) return immediately. They would return “request handles” that can be tested or waited on. The request handles can be waited on by calling MPI_Wait (or MPI_Waitall) and will return when data are ready.

Collectives

We introduce more MPI collectives operations. Collective operations are called by ALL processes in a communicator.

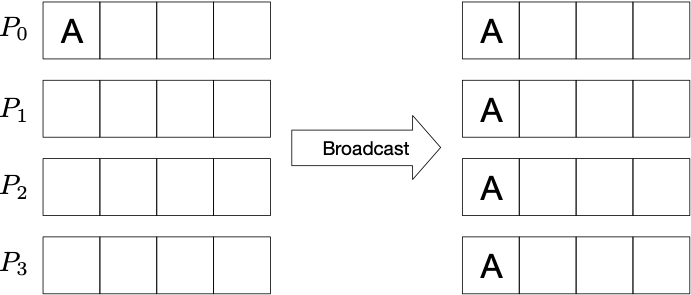
Broadcast:

../_images/bcast.png

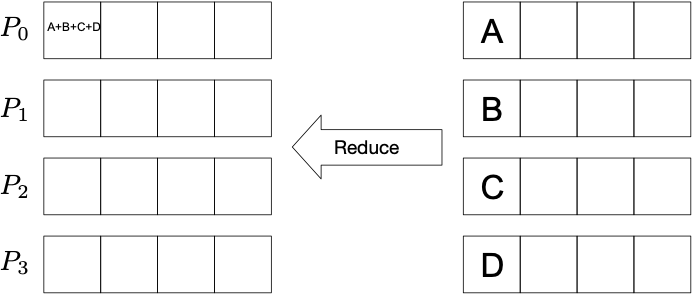
Reduce:

../_images/reduce.png

Allreduce:

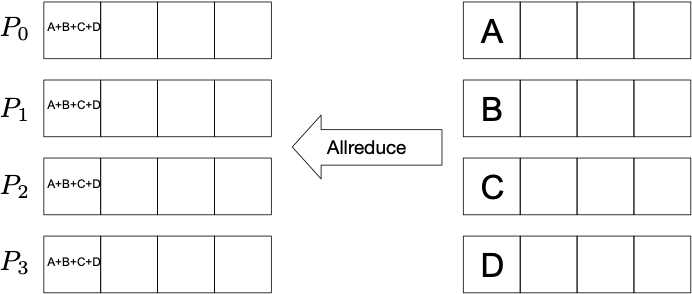
../_images/allreduce.png

Scatter/gather:

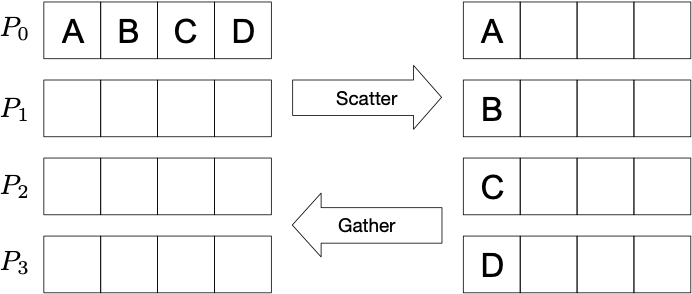
../_images/scatter-gather.png

Allgather:

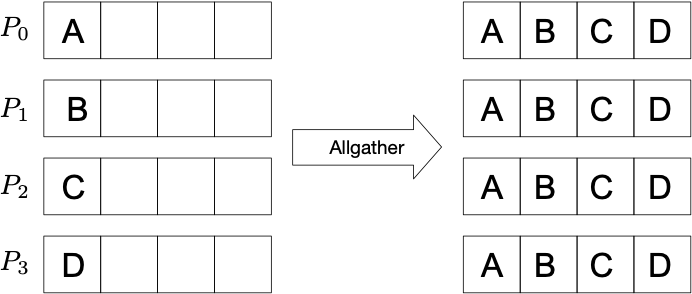
../_images/allgather.png

Alltoall:

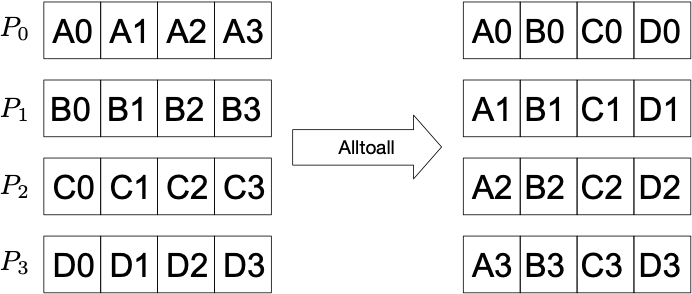
../_images/alltoall.png

Performance model

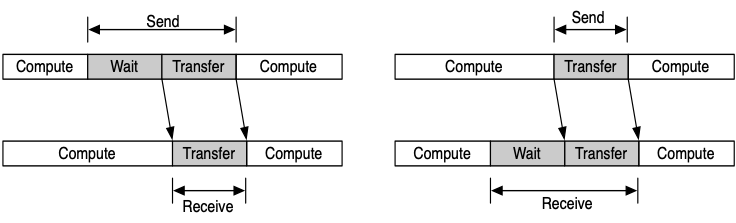
We provide a formula to evaluate the performance of MPI programs.

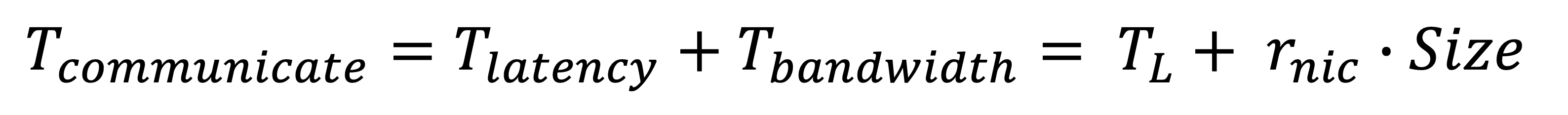
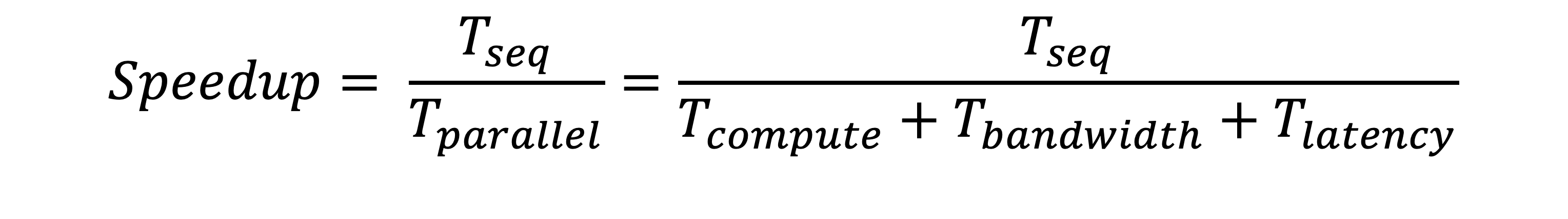
../_images/t_comm.png ../_images/t_speed.png

Here we compare synchronous BSP model with asynchronous BSP model.

../_images/comm.png

Eigenfaces

At the end, we introduce the background of the eigenface problem for the final assignment.

Given a training set of faces, we want to find an orthonormal basis that can form an alternate representation of faces with as few dimensions as possible. The axes are the “principal components”. First axis captures as much of the data set as possible, next axis captures as much of the data that isn’t captured by first, and so on. Based on this approach, we can represent any face with linear combination of the principal components.

To summerize, the major steps in the eigenfaces application are:

  1. Read in face images

  2. Compute mean face image

  3. Subtract mean from all face images

  4. Compute covariance matrix

  5. Compute eigendecomposition of covariance matrix

  6. Save eigenface images