Lecture 18: Message Passing¶




(Recorded 2022-05-26)
We continue to develop the message passing paradigm for distributed memory parallel computing, looking in more depth at principal abstractions in MPI (communicator, message envelope, message contents) and two vairants of “six-function MPI”. Laplace’s equation is part of the HPC canon so we do a deep dive on approaches for solving Laplace’s equation (iteratively) with MPI – which leads to the the compute-communicate (aka BSP) pattern.
MPI mental model¶
MPI mental model is about principal abstractions in MPI (communicator, message envelope, message contents). All MPI communication takes place in the context of an MPI Communicator. An MPI Communicator contains an MPI Group. The size of a communicator is the size of the group. Processes can query for size and for their own rank in group. An MPI Group translates from rank in the group to actual process. We us the index of a process in the group to identify other processes. Only processes in the group can use the communicator. All processes in the group see an identical communicator.
Six Function MPI Point to Point Version¶
We introduce six functions in MPI that allows us to do point to point message passing in the below figure.
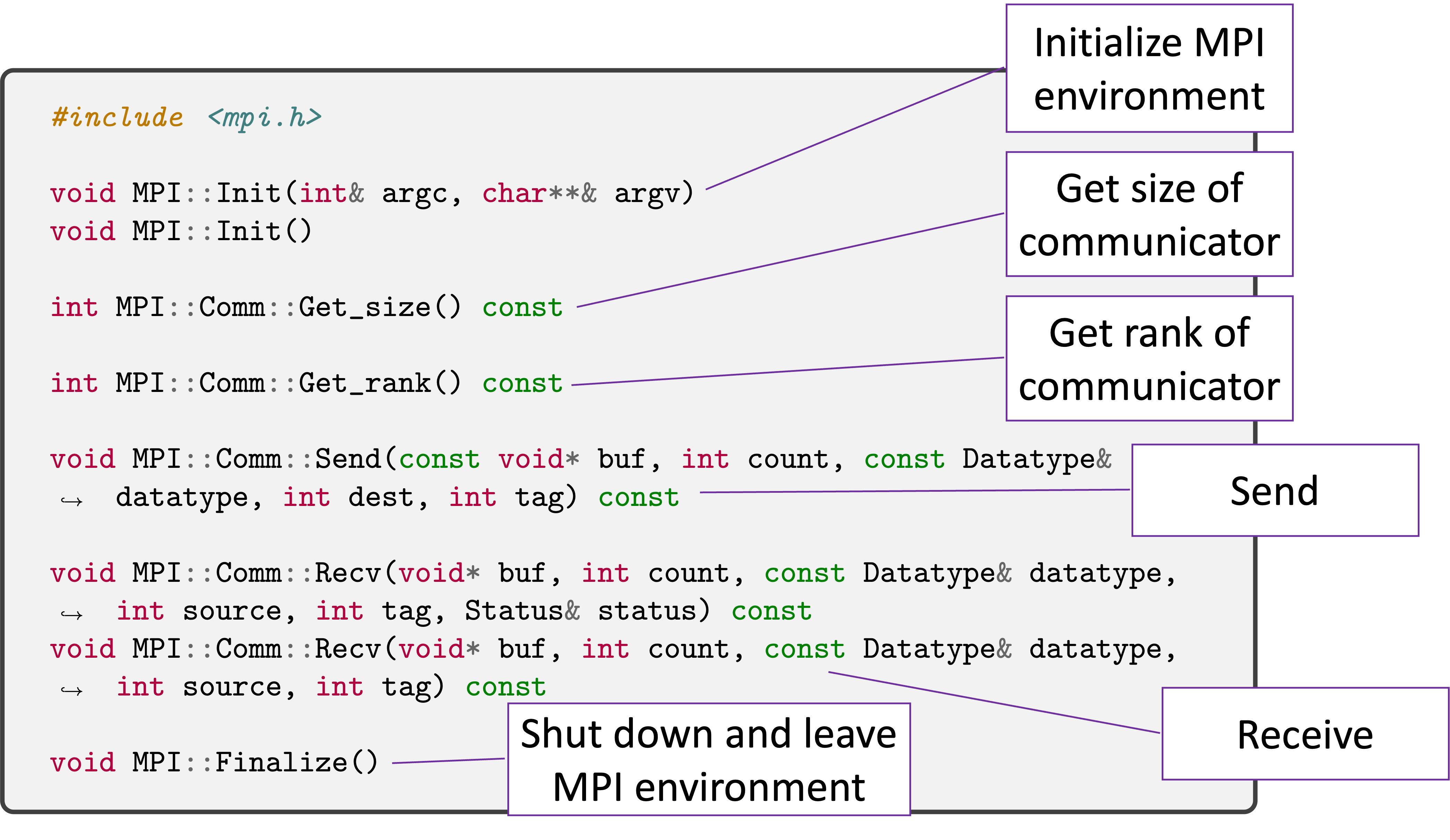
By using them in a Pingpong example, we demonstrate how these functions are used.
Six Function MPI Collective Version¶
In addition, we also introduce six functions in MPI that allows us to do collective message passing in the below figure.
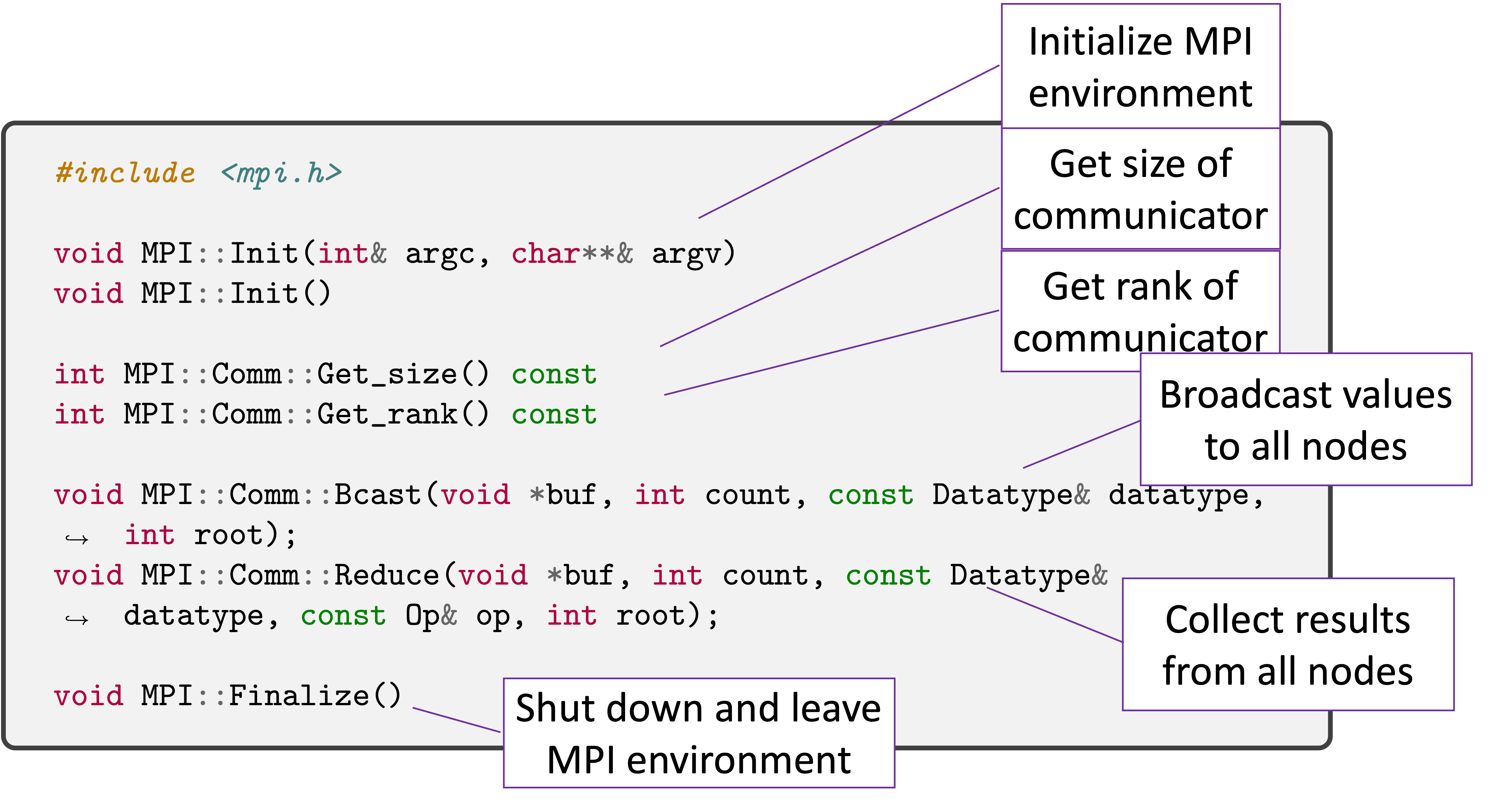
We also demonstrate how to use them to solve a Laplace’s equation iteratively n a regular grid using the above collective functions. Here we notice that the send / recv functions we introduce in this lecture are blocking send and receive. For receive, it only blocks until the buffer is safe to reuse. For send, it will block until message is received. On return from call, buffer will have message data.
We will continue the topic in MPI but introduce non-blocking version of send/recv in the next lecture with the same example.