Lecture 14: OpenMP¶

OpenMP programming model¶

We first introduce the execution model of OpenMP. An OpenMP program starts at the sequential region with one main thread. Then when it meets a parallel region, a thread team would be forked. Within the paralel region, the work would be done by multiple threads in parallel. Once the parallel region ends, all the threads in the thread team would be joined. The program returns to its sequential region with the main thread.

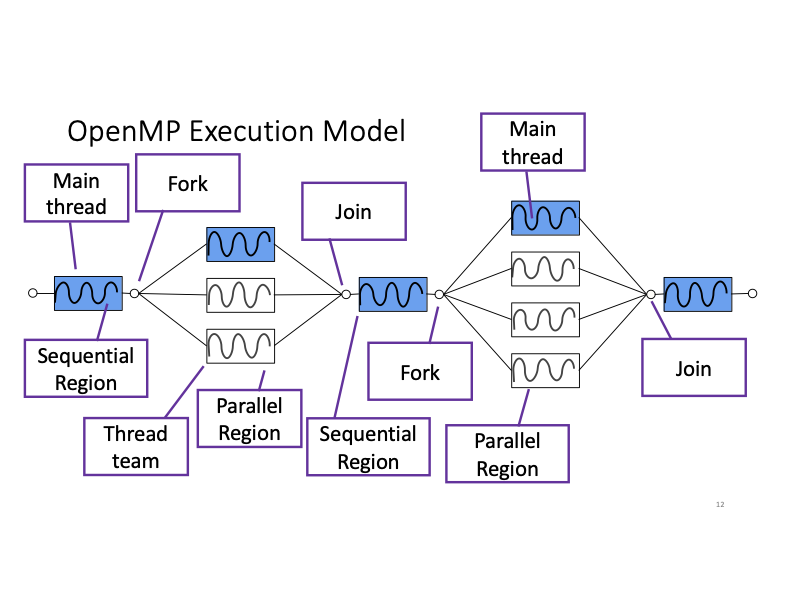
Programming with OpenMP¶

Let’s take a look at how to program with OpenMP.

We use #pragma omp parallel to start a parallel region in OpenMP. After we start a parallel region, how can we find out or even set the number of threads in current thread team?

OpenMP environment¶

To query the OpenMP environment, omp_get_num_threads() returns the number of threads in the current team. omp_get_max_threads() returns an upper bound on the number of threads that could be used.

To set the OpenMP environment, specifically to set the number of threads in a thread team, we can use omp_set_num_threads(num_threads). It affects the number of threads to be used for subsequent parallel regions. An alternative is to use an OpenMP Environment Variable - OMP_NUM_THREADS. We can set the environment variable as follow:

export OMP_NUM_THREADS=<number of threads to use>

Sometimes, we also have the need to query the thread id of each thread in the thread team. omp_get_thread_num() returns the thread number, with in the current team, of the calling thread.

Now we are familiar with the basics of OpenMP, let’s take a look at an exmaple - find the value of \(\pi\). How can we parallelize it using OpenMP?

Find the value of \(\pi\)¶

In previous lectures, we have taken a look at approximating the value of \(\pi\).

We use the following fomula to approximate the value of \(\pi\):

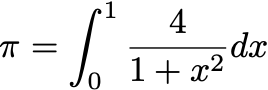
Using numerical quadrature method, we have

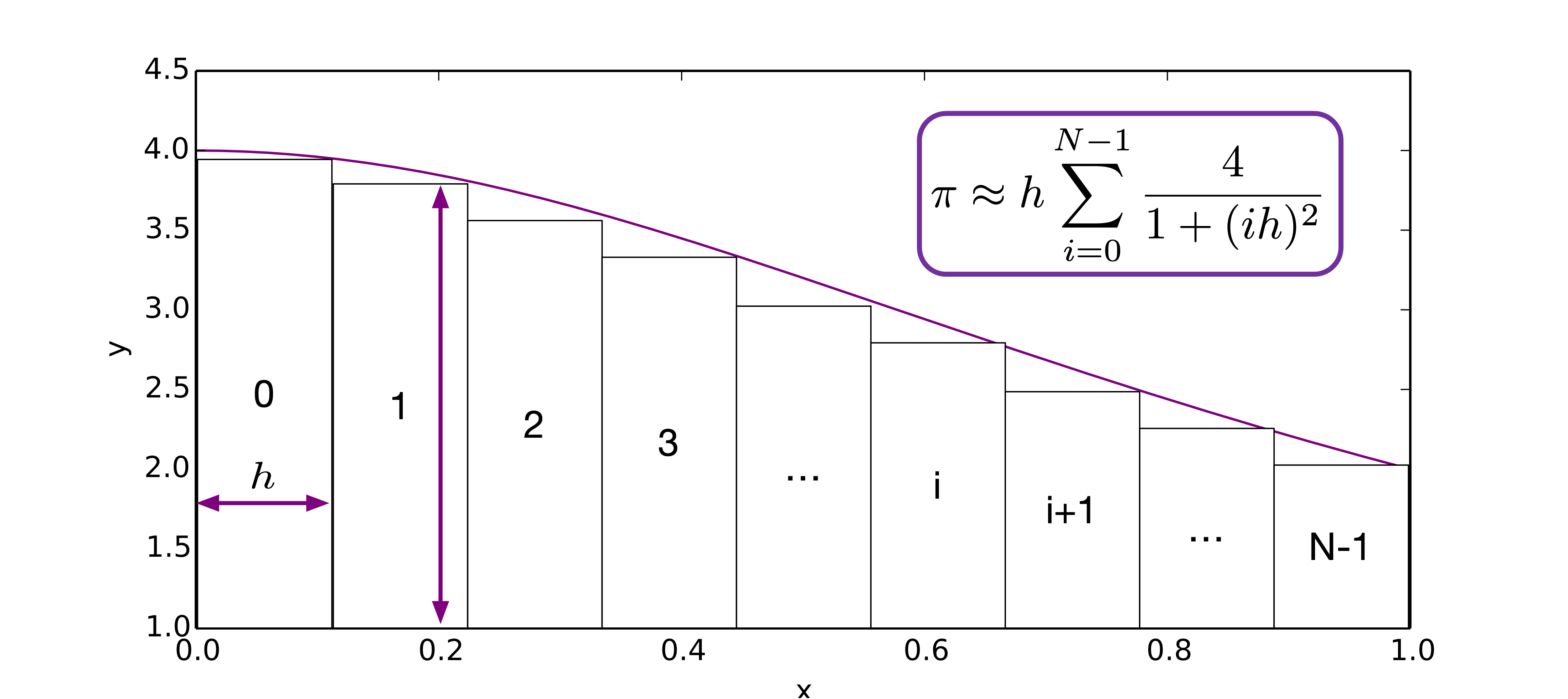
We find that the partial sums are all independent, and can be computed concurrently. How can we parallel it using OpenMP?

In this lecture, we start with #pragma omp parallel to create a parallel region in the computation of the value of \(\pi\). However, the output of this version shows that this version is not scalable. It turns out in the parallel region, each thread of the thread team would execute the same code in the parallel region. After we create a parallel region after #pragma omp parallel, each thread would create a private pi copy from the global pi, then do the computation on its own private copy. Next, after the computation, it performs read/write on the private version. After the parallel region ends, each thread would copy its private pi copy back to original pi. Therefore in this version, every thread is doing redundant work by repeating the computation for t times (t is the number of threads in the thread team in the parallel region).

To split the work among threads in the parallel region, we use #pragma omp parallel for to parallelize our for loop, and divides loop iterations between the spawned threads. In this version however, it turns out there is a race condtion on pi at the end of the parallel region. Because each thread is working on partial pi value, at the end of the parallel region, each thread would copy its private pi copy back to original pi at the same time. This causes the original pi to have a race condition.

To solve the race condition on the original pi, we introduce reduction clause - #pragma omp reduction to collaborate with #pragma omp parallel for. In this final version, #pragma omp parallel would sprawn a team of threads; then each thread will execute the parallel region; then #pragma omp parallel for would divides loop iterations between the spawned threads; finally, #pragma omp parallel for reduction(+:pi) would sum every private copy of pi up in parallel to the original pi.

Based on this method, we also parallelize our two_norm using OpenMP.

Additional resources¶

A good resource for learning OpenMP is OpenMP API Specification.

Another one is a “Hands-on” tutorial Introduction to OpenMP by Tim Mattson.

You are welcomed to share your OpenMP learning resources on Piazza with your classmates.