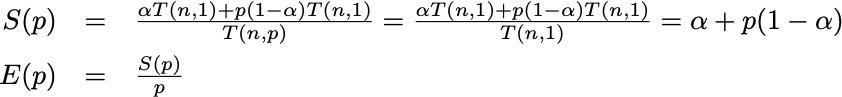Lecture 11: Shared Memory Parallelism, Correctness, Performance¶

Find the value of \(\pi\)¶

We use the following fomula to approximate the value of \(\pi\):

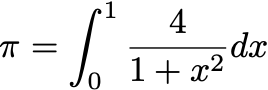
Using numerical quadrature method, we have

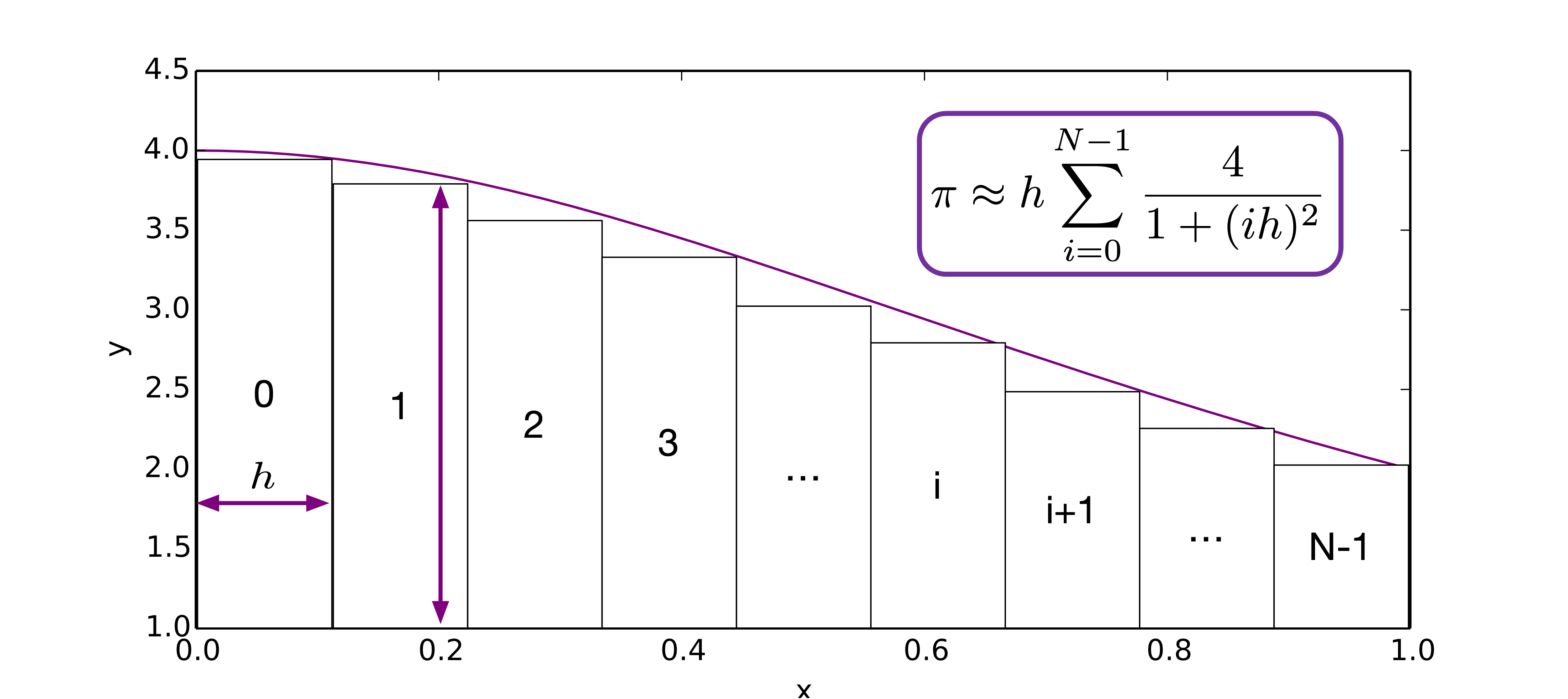
We find that the partial sums are all independent, and can be computed concurrently. But diving deep into a basic sequential solution, we come up with this partial_pi function as an independent task that can be computed using std::thread.

However, there is an unexpected error arises during the execution of our program.

Race condition¶

An unexpected error arises (or can arise) from concurrent accesses to shared variables: race condition.

We give another example - Bonnie and Clyde Use ATMs - to demonstrate the race condition and the critical section problem.

Critical Section Problem¶

We discuss the critical section problem and a couple of approaches for solving it.

The critical section problem is when n processes all competing to use some shared data, each process has a code segment, called critical section, in which the shared data is accessed. The key of the problem is to ensure that when one process is executing in its critical section, no other process is allowed to execute in its critical section.

There are three conditions for the solutions of the critical section problem:

• Mutual Exclusion - If process Pi is executing in its critical section, then no other processes can be executing in their critical sections

• Progress - If no process is executing in its critical section and there exist some processes that wish to enter their critical section, then the selection of the processes that will enter the critical section next cannot be postponed indefinitely

• Bounded Waiting - A bound must exist on the number of times that other processes are allowed to enter their critical sections after a process has made a request to enter its critical section and before that request is granted

Scalabiity¶

Scalabiity is a fundamental concept in high-performance computing. We introduce scalability via Amdahl’s law and Gustaffson’s law (strong and weak scaling, respectively).

Amdahl’s law (Strong Scaling)¶

Amdahl’s law gives the theoretical speedup in latency of the execution of a task at fixed workload that can be expected of a system whose resources are improved. By knowning the portion of the sequential program, we can use Amdahl’s law to predict the theoretically achievable speedup using multiple processors.

Assuming \(n\) is the size of the problem, \(\alpha\) is a ratio between 0 and 1 (the serial portion of the program), the runtime of the sequential program running on a single processor is the sum of these two parts:

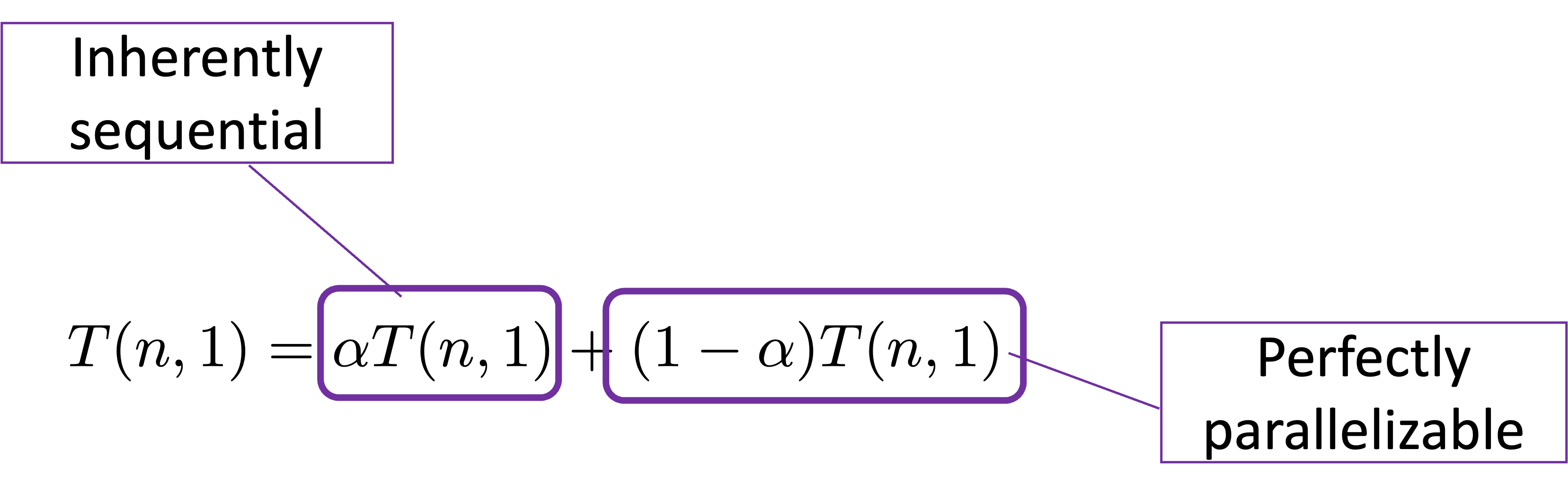
The parallelizable fraction can run \(p\) times faster on \(p\) processors while the serial faction remains the same:

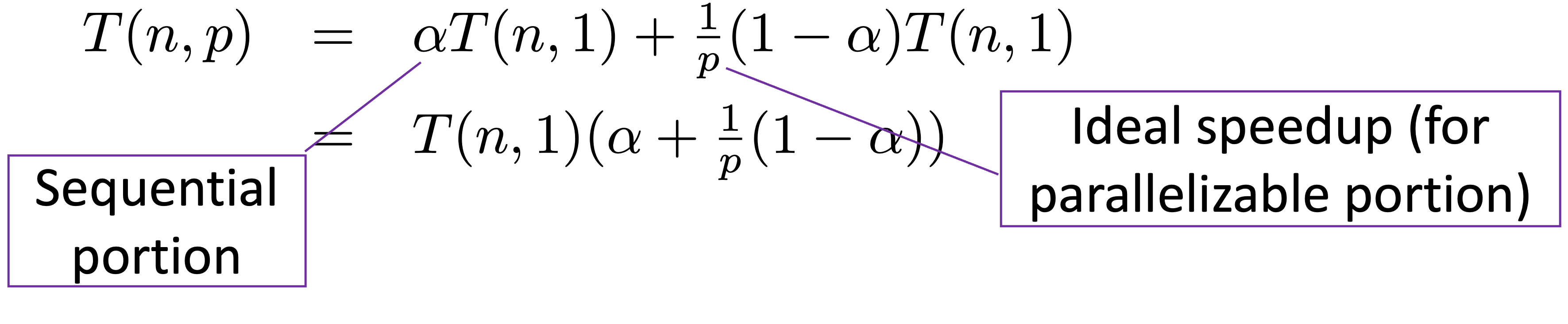
By dividing \(T(n, 1)\) by \(T(n, p)\), this results in an upper bound for the achievable speepup \(S(p)\) using \(p\) processors, hence we have Amdahl’s law:

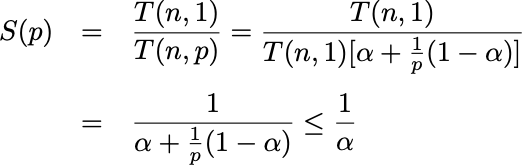
Gustaffson’s law (Weak Scaling)¶

Gustafson’s law gives the speedup in the execution time of a task that theoretically gains from parallel computing, using a hypothetical run of the task on a single-core machine as the baseline. By knowning the portion of the sequential program, we can use Gustaffson’s law to predict the theoretically achievable speedup using multiple processors when the parallelizable part scales linearly with the problem size while the serial part remains constant.

Assuming \(n\) is the size of the problem, \(\alpha\) is a ratio between 0 and 1 (the serial portion of the program), the runtime of the sequential program running on a single processor is the sum of these two parts:

If we guareentee that \(T(n, 1) = T(n, p)\), aka, the parallelizable grows linear in \(p\) while the non-parallelizable part remains constant, we have Gustaffson’s law: