Problem Set #4¶

Extract the homework files¶

Create a new subdirectory named “ps4” to hold your files for this assignment. The files for this assignment are in a “tar ball” that can be downloaded with ps4.tar.gz.

To extract the files for this assignment, download the tar ball and copy it (or move it) to your ps4 subdirectory. From a shell program, change your working directory to be the ps3 subdirectory and execute the command

$ tar zxvf ps4.tar.gz

The files that should be extracted from the tape archive file are

• Makefile:

• Matrix.hpp: Declarations for Matrix class

• Questions.rst: File containing questions to be answered for this assignment

• Timer.hpp: Simple timer class

• Vector.hpp: Declarations for Vector class

• amath583.cpp: Definitions (implementations) of Matrix and Vector functions

• amath583.hpp: Declarations of Matrix and Vector functions

• bandwidth.cpp: Simple program to (attempt to) measure CPU bandwidth

• blur.hpp: Definitions of blurring kernels

• catch.hpp: Catch2 testing framework header

• cpuinfo583.cpp: Simple program to read CPU flags

• kernels.hpp: Implementations of kernels with different numerical intensity

• mmult.cpp: Driver program for benchmarking matrix-matrix product with six different loop orderings

• mmult_ps3.cpp: Driver program for benchmarking matrix-matrix products from PS3

• mmult_ps3_test.cpp: Test program for verifying matrix-matrix products from PS3

• mmult_test.cpp: Test program for verifying matrix-matrix product with six different loop orderings

• mmult_trans.cpp: Driver program for benchmarking matrix-matrix transpose product with six different loop orderings

• mmult_trans_test.cpp: Test program for verifying matrix-matrix product transpose with six different loop orderings

• roofline.cpp: Simple program to (attempt to) measure CPU roofline parameters

• soa_image.hpp, aos_image.hpp, tensor_image.hpp: Definitions for different color image format structures

• soa_test.hpp, aos_test.hpp, tensor_test.hpp: Test programs for blurring kernels

• verify-all.bash: Meta bash script for running other verifiers

• verify-make.bash: Bash script that attempts to make all matrix programs for PS4

• verify-opts.bash: Bash script that sets options for other scripts

• verify-run.bash: Bash script that attempts to make and run all matrix timing programs for PS4

• verify-test.bash: Bash script that attempts to make and run all matrix test programs for PS4

More make automation¶

Although we can use macros in a Makefile to help make the content of our rules consistent, if you read through the Makefiles in the previous assignment, you will quickly notice that there is still a huge amount of repetition in each Makefile.

One place where there is alot of repetition is in the rule for building a .o file from a .cpp file. If you look at the Makefile from the previous assignment, you will see a sequence of rules that look like (this is just a few from that file)

hello.exe     : hello.cpp
                $(CXX) $(CXXFLAGS) hello.cpp -o hello.exe

goodbye.exe   : goodbye.cpp
                $(CXX) $(CXXFLAGS) goodbye.cpp -o goodbye.exe

mmtime.o      : mmtime.cpp Matrix.hpp amath583.hpp
                $(CXX) $(CXXFLAGS) -c mmtime.cpp -o mmtime.o

mnist.o       : mnist.cpp Matrix.hpp amath583.hpp
                $(CXX) $(CXXFLAGS) -c mnist.cpp -o mnist.o

mmtime.exe    : mmtime.o amath583.o
                $(CXX) $(CXXFLAGS) mmtime.o amath583.o -o mmtime.exe

mnist.exe     : mnist.o amath583.o
                $(CXX) $(CXXFLAGS) mnist.o amath583.o -o mnist.exe

But we can immediately see three patterns: a rule to create “something.exe” from “something.cpp”, a rule to create “something.o” from “something.cpp”, and a rule to create “something.exe” from “something.o” (plus other .o files).

If you want to add a new program to this project, you can write a new set of rules for it – but they will be exactly the same as a previous program, so you may end up cutting and pasting to save time and effort. In either case, there is lots of repetition – and if you make a change to the rule itself, you have to change it everywhere.

Let’s take a closer look at one of the patterns – the pattern for making a .o from a .cpp. All of those rules look like this:

<something>.o: <something>.cpp
            $(CXX) $(CXXFLAGS) -c <something>.cpp -o <something>.o

The dependency is that the something.o depends on the something.cpp (and maybe other files, we’ll come back to that later). If the dependency needs to be satisifeied, the compilation command (already parameterized with CXX and CXXFLAGS) is specified on the following line.

It would be really nice if we could create just one rule and apply to anything matching a specified pattern.

Fortunately, to automate pattern-based production rules, make has some “magic” macros that pattern match for you – namely $< and $@. The macro $< represents the file that is the dependency (the .cpp file) and $@ represents the target (the .o file).

A generic compilation statement would therefore be

<something>.o : $(CXX) -c $(CXXFLAGS) $< -o $@

That is, given a dependency rule that has a source file and a dependent target file (which is what all dependency rules have), this generic rule will substitute $@ with the target file and $< with the dependency.

That is, where we previously had the rules

mmtime.o      : mmtime.cpp Matrix.hpp amath583.hpp
                $(CXX) $(CXXFLAGS) -c mmtime.cpp -o mmtime.o

mnist.o       : mnist.cpp Matrix.hpp amath583.hpp
                $(CXX) $(CXXFLAGS) -c mnist.cpp -o mnist.o

We can now say

mmtime.o      : mmtime.cpp Matrix.hpp amath583.hpp
         $(CXX) -c $(CXXFLAGS) $< -o $@

mnist.o       : mnist.cpp Matrix.hpp amath583.hpp
         $(CXX) -c $(CXXFLAGS) $< -o $@

(And similarly for all the other rules for producing a .o).

That’s a good first step, but there are a few more things we need to clean up. First, there is an issue with the $< macro. Namely, which dependency is the one that we will compile to make the target? Most .o files have a large number of header files that they depend on. Above, for example, mnist.o depends not just on mnist.cpp but also on Matrix.hpp and amath583.hpp. If a recompile rule gets triggered because one of those changes, we want to compile the .cpp files that includes the .hpp file, not the .hpp file itself. To disambiguiate this situation, if we give a rule a list of dependencies, make will pick the first file as the one to pass to $<, so as long as we put the .cpp file first in the list, we will be okay.

Another approach, and the one we will be using for reasons that will become clear, is to note that dependencies are accumulated. You don’t need to specify all of them on one line. For instance, these are two equivalent ways of expressing the same dependencies:

# First way
norm.o: norm.cpp Vector.hpp amath583.hpp
        $(CXX) -c $(CXXFLAGS) $< -o $@

# Second way
norm.o: Vector.hpp amath583.hpp
norm.o: norm.cpp
        $(CXX) -c $(CXXFLAGS) $< -o $@

# Third way
norm.o: norm.cpp
        $(CXX) -c $(CXXFLAGS) $< -o $@

norm.o: Vector.hpp
norm.o: amath583.hpp

Note that in the second and third way the production rule for the .o is more obvious. There is just one dependence. But, whenever any of the dependencies are out of date, the production rule will get fired, and since the .cpp and .o rule are right above the production rule, and since there is just the one binding, it is more obvious what will get bound to $<.

There is one last thing to clean up here. We still have a repetitive pattern – all we did was substitute the magic macros in. But every production rule still has:

something.o : something.cpp
        $(CXX) -c $(CXXFLAGS) $< -o $@

We haven’t really saved any lines of Makefile, or eliminated any actual repetitions – we just made on of the repetitions (the production rule) exactly the same everywhere.

But that the rule is exactly the same everywhere cries out even more for automation. In fact, there is one last piece of pattern-matching that make has and that will let us roll all of those rules up into just one: implicit rules. We express an implicit rule like this:

%.o : %.cpp
        $(CXX) -c $(CXXFLAGS) $< -o $@

This basically the rule with “something” above where the % stands in for “something”. We only need to write this rule once and it covers all cases where something.o depends on something.cpp. We still have the other dependencies (on headers) to account for – but this can also be automated (more on that in the next assignment).

At any rate, the Makefile we started with now looks like this:

CXX      = c++
CXXFLAGS = -Wall -g -std=c++11

# Implicit rule for building .o from .cpp
%.o : %.cpp
         $(CXX) -c $(CXXFLAGS) $< -o $@

# Dependencies
amath583.o: amath583.hpp
amath583.o: Vector.hpp
norm.o: amath583.hpp
norm.o: Vector.hpp

This will handle all cases where something.o depends on something.cpp. Using these magic macros and implicit rules greatly simplifies what we have to put in a Makefile and it also allows us to separately specify dependencies from production rules. (Note also that the dependency of, say, amath583.o on amath583.cpp is covered by the implicit rule, so we only need to explicitly specify other dependencies, the header files).

NB: We will still continue to supply Makefiles for much of your assignments, but we will be gradually taking some of the scaffolding away in future problem sets and you may have to add rules for your own files. You can add those rules however you like, you do not have to use any of the advanced features of make in your assignments as long as your programs correctly build for the test script(s). However, these features were created to make the lives of programmers easier, so you will probably find it useful to familiarize yourself with these rules so that you can take advantage of them.

cpuinfo¶

As discussed in lecture, the SIMD/vector instruction sets for Intel architectures have been evolving over time. Although modern compilers can generate machine code for any of these architectures, the chip that a program is running on must support the instructions generated by the compiler. If the CPU fetches an instruction that it cannot execute, it will throw an illegal instruction error.

The machine instruction cpuid can be used to query the microprocessor about its capabilities (cf. CPUID). How to issue these queries and how to interpret the results is explained (e.g.) in the wikipedia entry for cpuid. A small program for querying your machines CPU in this way is provided in “cpuinfo583.cpp”. The program interacts directly with the CPU using assembly language instructions (in particular the cpuid instruction).

Compile and run cpuinfo583.exe (there is a rule for it in your Makefile).

$ make cpuinfo583.exe
$ ./cpuinfo583.exe

You will get a listing that shows a selection of available capabilities on your own machine. Run this command and check the output. The particular macros to look for are anything with “SSE”, “AVX”, “AVX2”, or “AVX512”. These support 128-, 256-, 256-, and 512-bit operands, respectively.

What level of SIMD/vector support does the CPU your computer provide?

What is the maximum operand size that your computer will support?

What is the minimum operand size that your computer will support?

What is the clock speed of your CPU? You may need to look this up via “About this Mac” on MacOSX. If your Macbook is using Apple M1 Chip, try “sudo powermetrics” in the terminal, looking for “CPU frequency”. Look at the “Performance” Tab in Task Manager on a Windows; and try “lscpu” in the terminal on a Linux.

Roofline¶

In lecture 8 we presented the roofline model, which provides an upper bound to computational performance, taking into account both potential floating point performance as well as the ability of the system to supply enough operands to the CPU to do its computations (bandwidth). A roofline model can be plotted on a graph of performance (in GFlops/sec) as a function of “numerical intensity” (flops/byte). The limitations on computational performance (in GFlops/sec) are horizontal lines on the graph, while bandwidth (bytes/sec) is a sloped line. For example (measured on my laptop):

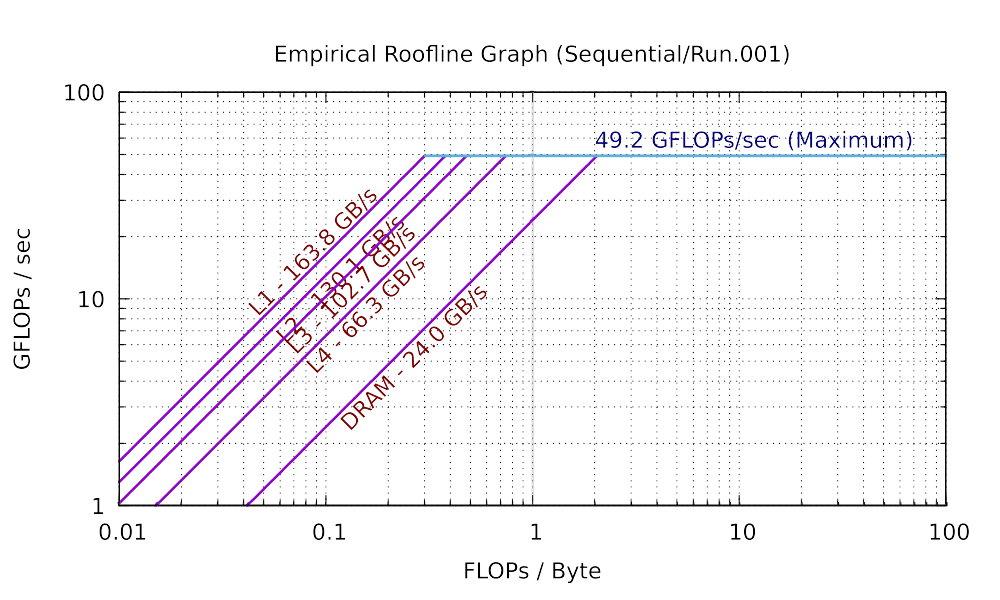
As we have also discussed in lecture, your computer doesn’t have a single bandwidth. The bandwidth between L1 cache and the CPU is significantly faster than the bandwidth between main memory and the CPU. The performance of your program therefore depends also on the problem size as well as the numerical intensity.

For this part of this assignment I want you to continue developing an intuition for what affects (and effects) performance on your computer (or any computer). There isn’t a “right answer” for this part. Every computer system is different – and, as we have seen, trying to suss out different aspects of your computer’s performance is complicated – made even more so by the compiler (which are subtle and quick to anger).

But what I want you to for this part is to create a roofline model for your computer – again, there isn’t a right answer.

For the roofline model you will need to characterize a few things. First is the peak available performance for your computer (for now we will just be looking at peak performance available with a single core). The second is the bandwidth – for L1, L2 (if present), L3 (if present), L4 (if present), and main memory (DRAM).

Below are some experiments to do to help determine these parameters for your computer. For each of bandwidth and for roofline there are two approaches: “homegrown” and “docker”. The former uses a C++ program that you build and run on your computer. The second builds and runs a more sophisticated set of experiments within a docker container. Which approach you want to use is up to you (and you can do both).

To setup a homegrown develop environment, you can follow the material in Set Up Your Development Environment (Without Docker) in the “excursus” section of the course web site.

Bandwidth: Homegrown¶

Your ps4 directory contains a program “bandwidth.cpp” which you can compile to “bandwidth.exe”. This program runs some simple loops to try to measure bandwidth for reading, writing, and copying (reading and writing). The functions that carry out the loops are parameterized by the size of the data to work on as well as by the number of trials to run within the timing loop:

// Reading
for (size_t j = 0; j < ntrials; ++j) {
  for (size_t i = 0; i < A.size(); ++i) {
    a = A[i];
  }
}

// Writing
for (size_t j = 0; j < ntrials; ++j) {
  for (size_t i = 0; i < A.size(); ++i) {
    A[i] = a;
  }
}

// Copying
for (size_t j = 0; j < ntrials; ++j) {
  for (size_t i = 0; i < A.size(); ++i) {
    B[i] = A[i];
  }
}

The main program will in turn invoke the timing loops for problem sizes ranging from 128 bytes up to 128MB (you can specify a different upper limit on the command line).

Build this program and run it with no arguments (or with something larger than 128M)

$ make bandwidth.exe
$ ./bandwidth.exe
$ ./bandwidth.exe 268435456

Multiple columns of data will scroll by. The first set are for reading, the second for writing, the third for copying. The main number of interest is in the final column – bytes/second – aka your bandwidth.

For example, a few selected lines from running this program on my laptop look like this:

bytes/elt  #elts  res_bytes  ntrials    usecs      ttl_bytes      bytes/sec

8         256        4096   2097156     45000     8589950976    1.90888e+11
8         512        8192   1048580     41000     8589967360    2.09511e+11
8        1024       16384    524292     38000     8590000128    2.26053e+11
8        2048       32768    131074     20000     4295032832    2.14752e+11
8        4096       65536     65538     69000     4295098368    6.22478e+10
8        8192      131072     32770     69000     4295229440    6.22497e+10

There is a major fall off between 32k and 64k bytes – indicating that L1 cache is (probably) 32k bytes. It also looks like L1 cache bandwidth is (probably) about 226GB/s.

Based on the output from bandwidth.exe on your computer, what do you expect L1 cache and L2 cache (if present) sizes to be? What are the corresponding bandwidths? How do the cache sizes compare to what “about this mac” (or equivalent) tells you about your CPU? (There is no “right” answer for this question – but I do want you to do the experiment.)

Bandwidth: Docker¶

Use docker to pull the image amath583/bandwidth (it has been put on docker hub). When running, this image will execute a profiling program put its results into a subdirectory called “BW”. So, before running this image, you will need to first create a subdirectory named BW in the directory that you have mapped to in docker. That is:

$ cd <your working directory>
$ mkdir BW
$ docker pull amath583/bandwidth
$ docker run -v <your working directory>:/home/amath583/work amath583/bandwidth

The <your working directory> stands for the location on your host machine where you have deen doing your work. The bandwidth program may run for quite some time – 10-20 minutes – during which time your computer should have as little load on it as possible (other than the bandwidth program itself).

When the program completes, there will be two files in the BW directory – bandwidth.bmp and bandwidth.csv. The file bandwidth.png is an image of a graph showing data transfer rates for various types of operations and various types of operations. The file bandwidth.csv is the raw data that is plotted in bandwidth.bmp, as comma separated values. You can use that data to do your own investigations about your computer.

An example of bandwidth.bmp from my laptop is the following (your results will most likely vary):

In looking at the bandwidth graph you can see one or more places where the transfer rate drops suddenly. For small amounts of data, the data can fit in cache closer to the CPU – and hence data transfer rates will be higher. The data transfer rates will fall off fairly quickly once that data no longer completely fits into cache.

Same questions as for the “homegrown” approach:

Based on the output from running this image on your computer, what do you expect L1 cache and L2 cache (if present) sizes to be? What are the corresponding bandwidths? How do the cache sizes compare to what “about this mac” (or equivalent) tells you about your CPU? (There is no “right” answer for this question – but I do want you to do the experiment.)

(You only need to do one of homegrown or docker.)

Roofline: Homegrown¶

In your ps4 directory is a program “roofline.cpp” which you can compile to “roofline.exe” (there should be make rule in your Makefile for it). This program does something similar to “bandwidth.cpp but rather than vary the problem size, it varies the arithmetic intensity for a fixed problem size (as specified by the command-line argument).

On my laptop when I run the program (e.g.) I see something like this:

 $ ./roofline.exe 128

kernel sz  res_bytes   ntrials      usecs      ttl_bytes         ttl_flops      intensity      flops/sec      bytes/sec
        2        128  33554433     114000     8589934848        1073741856          0.125    9.41879e+09    7.53503e+10
        4        128  16777217      80000     4294967552        1073741888           0.25    1.34218e+10    5.36871e+10
        8        128   8388609      63000     2147483904        1073741952            0.5    1.70435e+10     3.4087e+10
       16        128   4194305      55000     1073742080        1073742080              1    1.95226e+10    1.95226e+10
       32        128   2097153      52000      536871168        1073742336              2    2.06489e+10    1.03244e+10
       64        128   1048577      54000      268435712        1073742848              4    1.98841e+10    4.97103e+09

Compile and run this program, choosing a few problem sizes in the middle of each cache size (about half the cache size) and perhaps also try +- a factor of two. As with the bandwidth program above, you should see some plateaus for performance at different problem sizes.

At a problem size around half the L1 cache, you should see pretty large numbers for floating point performance with the middle number of arithmetic intensity. The largest number that you see for performance (at any level of arithmetic intensity and any problem size) is the horizontal line for the rooline characterization of your computer. The sloped lines that are also part of the model can be gleaned also from this program but may be more obvious from the bandwidth program.

What is the (potential) maximum compute performance of your computer? (The horizontal line.) What are the L1, L2 (if present), and DRAM bandwidths? How do those bandwidths correspond to what was measured above with the bandwidth program?

Based on the clock speed of your CPU and its maximum Glop rate, what is the (potential) maximum number of double precision floating point operations that can be done per clock cycle? (Hint: Glops / sec \(\div\) GHz = flops / cycle.) There are several hardware capabilities that can contribute to supporting more than one operation per cycle: fused multiply add (FMA) and AVX registers. Assuming FMA contributes a factor of two, SSE contributes a factor of two, AVX/AVX2 contribute a factor of four, and AVX contributes a factor of eight of eight, what is the expected maximum number of floating point operations your CPU could perform per cycle, based on the capabilities your CPU advertises via cpuinfo (equiv. lscpu)? Would your answer change for single precision (would any of the previous assumptions change)?

Not required if you use the homegrown approach, but I nevertheless encourage you to develop an approximate roofline model for your computer and plot it (similar to the plot above and shown in lecture).

Roofline: Docker¶

A docker image that will profile your computer and create a roofline plot has been put on docker hub:. One image is called: amath583/ert, which will create a roofline plot based on a single CPU core of your machine. When running, this image will put its results into a subdirectory called “ERT”. So, before running this image, first create a subdirectory named ERT in the directory you are mapping to docker.

To run the amath583/ert image:

$ cd <your working directory>
$ mkdir ERT
$ docker pull amath583/ert
$ docker run -v <your working directory>:/home/amath583/work amath583/ert

The <your working directory> stands for the location on your host that will be mapped to a directory inside of the container. This is not an interactive image, so you don’t need the “-it” option.

The roofline characterization will run for a few minutes, but probably not as long as the bandwidth characterization.

Once the image finishes, you will find results in the subdirectory named Sequential, under wich there will be one or more subdirectories with the name like Run.001. Directly in the Run.001 subdirectory will be a file roofline.pdf, which contains a graph of the roofline model for your computer.

NB: If you do multiple runs of the roofline profiler, delete the subdirectory Run.001 each time so that the profiler has a fresh directory to write to and there won’t be old or incomplete results to confuse you or to confuse the profiler.

What is the maximum compute performance of your computer? (The horizontal line.) What are the L1, L2 (if present), and DRAM bandwidths? How do those bandwidths correspond to what was measured above?

mult vs mult_trans¶

Your ps4 directory contains a benchmark driver mmult_ps3.cpp that exercises the matrix multiply and matrix multiply transpose operations we wrote in the last assignment. It loops over a set of matrix sizes (8 to 256) and measures the performance of each function at that size. For each size it prints a row of performance numbers in GFlops/sec – each column is the performance for one of the functions.

The functions mult_0 through mult_3 were provided for you last time and are included again. The functions mult_trans_0 through mult_trans_3 are empty – copy the versions over that you wrote last time. If you are not happy with the performance you got and would like to use an “approved” solution instead, contact one the TAs or ask a classmate. It is okay to copy those functions for this assignment only.

(Why am I not just providing those you may ask? All of ps1 through the final may ultimately be available at the same time. For those who may want to reuse this material (including my future self), I don’t want solutions for a given assignment to just be available from a future assignment.)

Compile and run mmult_ps3.exe (the default size used with no command line argument should be fine). There is a make rule that invokes the compiler with optimizations enabled so you should just be able to

$ make mmult_ps3.exe
$ ./mmult_ps3.exe

If your computer and compiler are more or less like mine, you should see something printed that looks like this:

  N      mult_0      mult_1      mult_2      mult_3     mul_t_0     mul_t_1     mul_t_2     mul_t_3
  8     3.00795     2.90768     6.23075     5.81536      3.6346     3.35502     7.93004     7.26921
 16     2.35758      2.4572     6.23075     6.12144     2.50123     6.58343     11.0769     11.8279
 32     1.98706     2.01804     6.61387     6.56595     2.29975     12.0813     15.8965      17.425
 64     1.70172     1.94222     6.08737     6.62057     2.05673     13.9541      20.156     17.7847
128     1.57708     1.72746     6.05582     6.35951     1.79506     14.7662      21.136      16.457
256     1.28681     1.46371     4.87796     5.92137     1.62958      11.073     19.4263     15.7063

Huh. Although we applied all of the same optimizations to the mult and mult_trans functions – the mult_trans functions are significatnly faster – even for the very simplest cases. That is fine, as for the last assignment, when you need to compute \(C = A\times B^T\) – but we also need to just be able to compute \(C = A\times B\) – it is a much more common operation – and we would like to do it just as fast as for \(C = A\times B^T\).

Save the output from a run of mmult_ps3.exe into a file mmult_ps3.log.

Loop Ordering¶

The mathematical formula for matrix-matrix product is

which we realized using our Matrix class as three nested loops over i, j, and k (in that nesting order). This expression says “for each \(i\) and \(j\), sum each of the \(A_{ik} B_{kj}\) products.

The function(s) we have been presenting, we have been using the “ijk” ordering, where i is the loop variable for the outer loop, j is the loop variable for the middle loop, and k is the loop variable for the inner loop:

void   mult(const Matrix& A, const Matrix& B, Matrix& C) {
  for (size_t i = 0; i < C.num_rows(); ++i) {
    for (size_t j = 0; j < C.num_cols(); ++j) {
      for (size_t k = 0; k < A.num_cols(); ++k) {
        C(i, j) += A(i, k) * B(k, j);
      }
    }
  }
}

But the summation is valid regardless of the order in which we add the k-indexed terms to form each \(C_{ij}\). Computationally, if we look at the inner term C(i,j) = C(i,j) + A(i,k)*B(k,j) – there is no dependence of i on j or k (nor any of the loop indices on any of the other loop indices); we can do the inner summation in any order. That is, we can nest the i, j, k loops in any order, giving us six variants of the matrix-matrix product algorithm. For instance, an “ikj” ordering would have i in the outer loop, k in the middle loop, and j in the inner loop.

void   mult_ikj(const Matrix& A, const Matrix& B, Matrix& C) {
  for (size_t i = 0; i < C.num_rows(); ++i) {
    for (size_t k = 0; k < A.num_cols(); ++k) {
      for (size_t j = 0; j < C.num_cols(); ++j) {
        C(i, j) += A(i, k) * B(k, j);
      }
    }
  }
}

$ make mmult.exe
$ ./mmult.exe

What is the Best Loop Ordering?¶

I claim that certain loop ordering give good performance because of the memory access pattern being favorable. Is that consistent with what you are seeing in these (unoptimized) functions?

To guide your discussion, consider the following diagram of matrices A, B, and C.

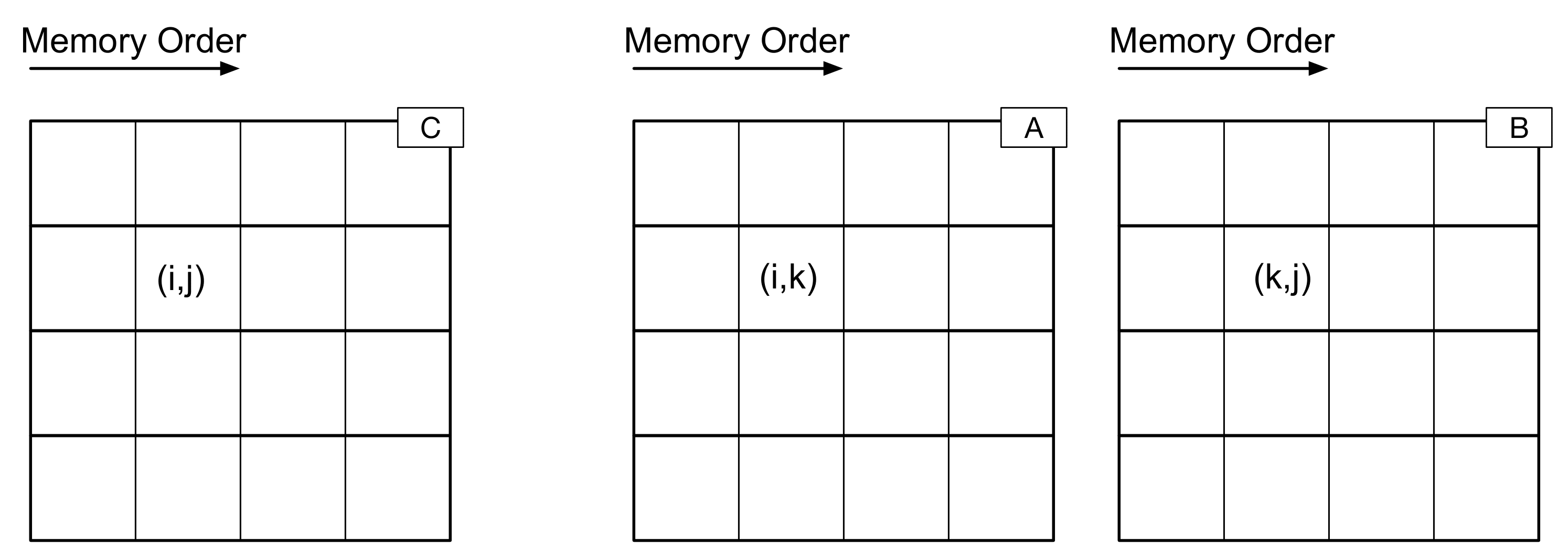
Here, each box is a matrix entry. Recall that for row-ordered matrices (such as we are using in this course), the elements in each row are stored next to each other in memory.

Now, let’s think about what happens when we are executing matrix multiply with the “ijk” ordering. From one iteration of the inner loop to the next (from one step of the algorithm to the next), what are the next data elements to be accessed? For “ijk”, here is what happens next:

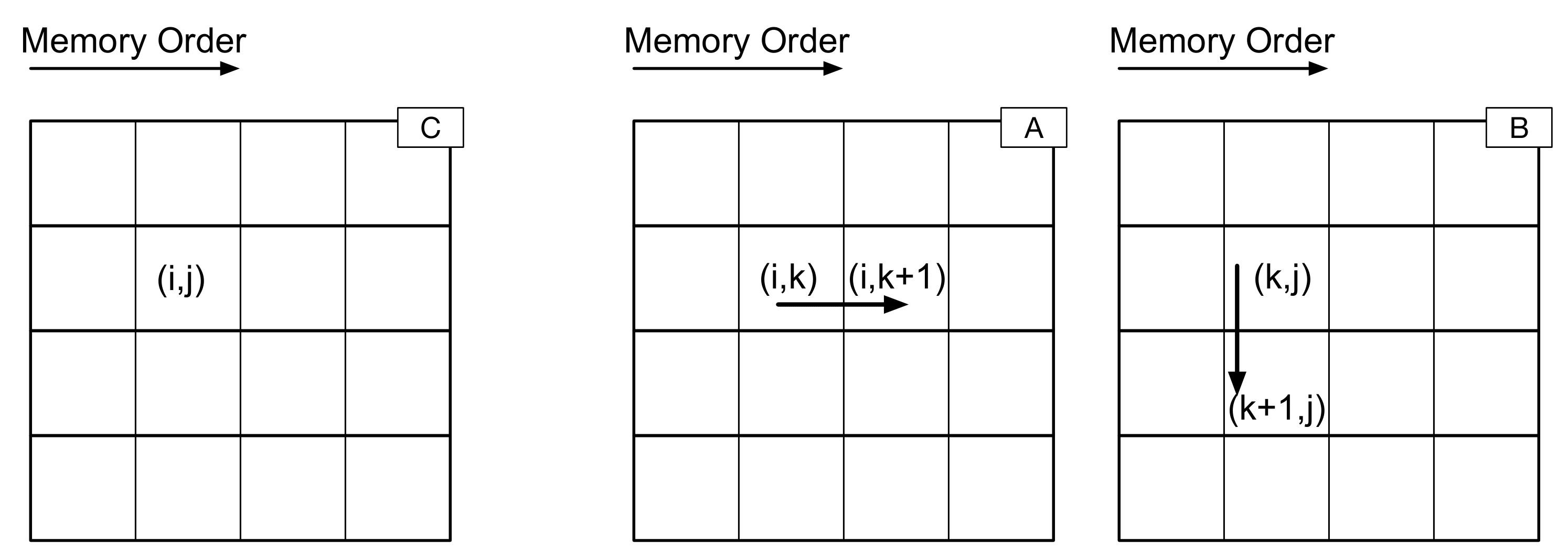
What happens in the case of each of the six orderings for mult – what are the next elements to be accessed in each case? Does this help explain the similarities between certain orderings – as well as why there are good, bad, and ugly (er, medium) pairs? Refer again to how data are stored for three matrices A, B, and C.

Referring to the figures about how data are stored in memory, what is it about the best performing pair of loops that is so advantageous?

#define 0
Stuff I want to save but not compile
#endif

Array of Structs vs Struct of Arrays¶

To store the “color” of a particular pixel, a color image stores the values of the three additive primar colors (red, green, and blue) necessary to reconstruct that color. A color image is thus a three-dimensional structure: 3 color planes, each of which is the same height by width of the image.

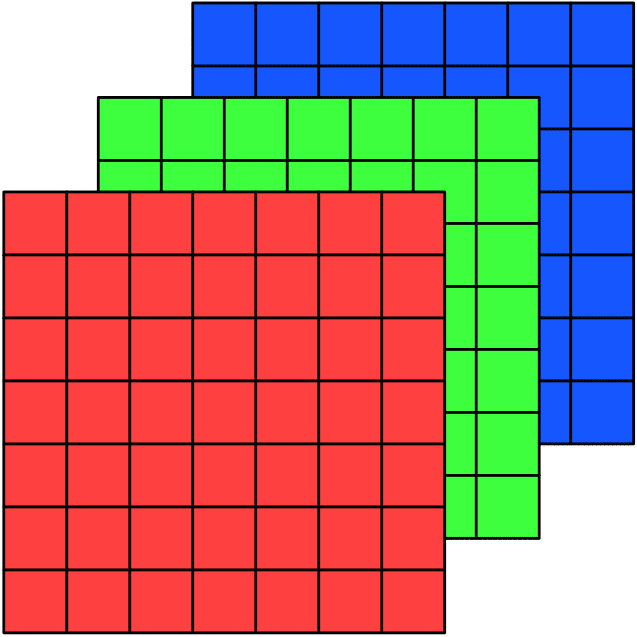
A question arises then about what is the best way to store / access that data in memory? We could, for instance, store each color plane separately, so that the image is a “structure of arrays”:

Or, we could store the three color values of each pixel together, so that the image is an “array of structures”:

Or, we could store just a single large array, treating the image as a “tensor” and use a lookup formula to determine how the data are stored.

The struct of arrays data structure could be implemented like this:

class SOA_Image {
public:
  SOA_Image(size_t M, size_t N)
      : nrows_(M), ncols_(N), storage_{{std::vector<double>(M * N), std::vector<double>(M * N), std::vector<double>(M * N)}} {}

  size_t num_rows() const { return nrows_; }
  size_t num_cols() const { return ncols_; }

  const double& operator()(size_t i, size_t j, size_t k) const { return storage_[k][i * ncols_ + j]; }
  double&       operator()(size_t i, size_t j, size_t k) { return storage_[k][i * ncols_ + j]; }

private:
  size_t                             nrows_;
  size_t                             ncols_;
  std::array<std::vector<double>, 3> storage_;
};

Again, the terminology “struct of arrays” is generic, referring to how data are organized in memory. Our implementation (in storage_) of the “struct of arrays” is as a array of vector. Note also that the accessor operator() accesses pixels with (i, j, k) where i and j are pixel coordinates and k is the color plane.

Similarly, the array of structs data structrue could be implemented this way:

class AOS_Image {
public:
  AOS_Image(size_t M, size_t N) : nrows_(M), ncols_(N), storage_(M * N) {}

  const double& operator()(size_t i, size_t j, size_t k) const { return storage_[i * ncols_ + j][k]; }
  double&       operator()(size_t i, size_t j, size_t k) { return storage_[i * ncols_ + j][k]; }

  size_t num_rows() const { return nrows_; }
  size_t num_cols() const { return ncols_; }

private:
  size_t                             nrows_;
  size_t                             ncols_;
  std::vector<std::array<double, 3>> storage_;
};

Again, the terminology “array of structs” is generic. Our implementation (in storage_) of the “array of structs” is as a vector of array. Note also that the accessor operator() accesses pixels with (i, j, k) where i and j are pixel coordinates and k is the color plane.

Finally, a “tensor” based storage could be implemented as:

class Tensor_Image {
public:
  Tensor_Image(size_t M, size_t N) : nrows_(M), ncols_(N), storage_(3 * M * N) {}

  const double& operator()(size_t i, size_t j, size_t k) const { return storage_[k * nrows_ * ncols_ + i * ncols_ + j]; }
  double&       operator()(size_t i, size_t j, size_t k) { return storage_[k * nrows_ * ncols_ + i * ncols_ + j]; }

  size_t num_rows() const { return nrows_; }
  size_t num_cols() const { return ncols_; }

private:
  size_t              nrows_;
  size_t              ncols_;
  std::vector<double> storage_;
};

Blurring¶

Although blurring an image sounds like something you would not want to do, small amounts of blur can be useful in image processing for, say, removing high frequency noise from an image. One simple blurring function is a box blur, which computes an output pixel based on the average of nine neighboring input pixels.

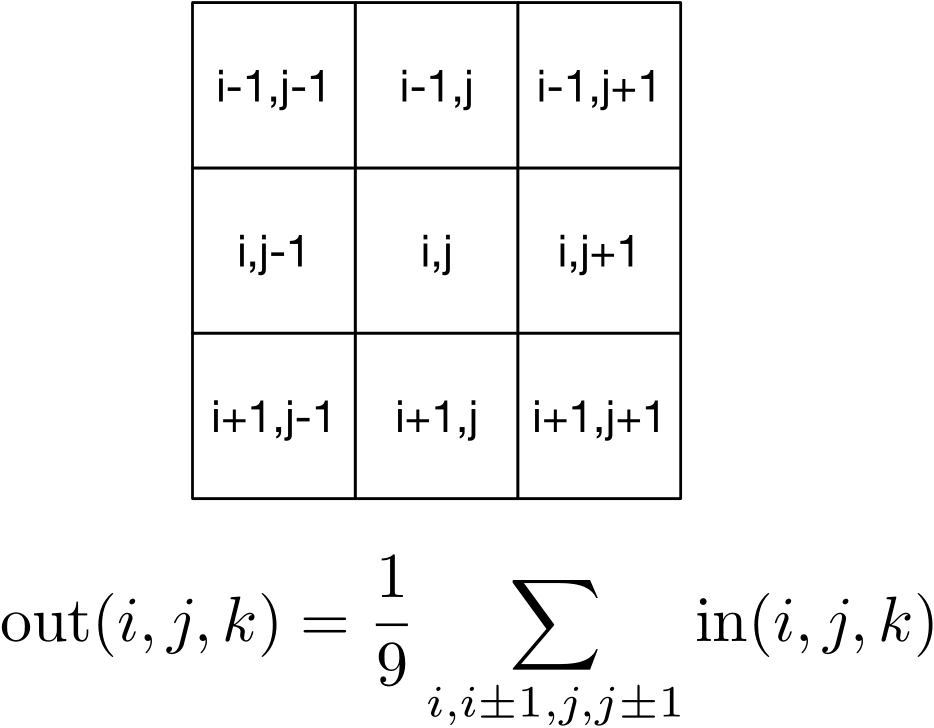
So, for instance, we could blur an image with the following:

// Iterate through the image
for (size_t i = 1; i < img.num_rows() - 1; ++i) {
  for (size_t j = 1; j < img.num_cols() - 1; ++j) {

    // Iterate through the color planes
    for (size_t k = 0; k < 3; ++k) {

      // Apply blurring kernel
      blurred(i, j, k) = (img(i + 0, j + 0, k) +
                          img(i + 0, j + 1, k) +
                          img(i + 0, j - 1, k) +
                          img(i + 1, j + 0, k) +
                          img(i + 1, j + 1, k) +
                          img(i + 1, j - 1, k) +
                          img(i - 1, j + 0, k) +
                          img(i - 1, j + 1, k) +
                          img(i - 1, j - 1, k)) / 9.0;
    }
  }
}

Note that since we have defined the accessor generically, the inner blurring kernel will be the same regardless of which representation we use for the image. We do have a choice, however in how we access the data: do we iterate over the color planes as the outer loop or as the inner loop?